各类梯度下降算法的演进

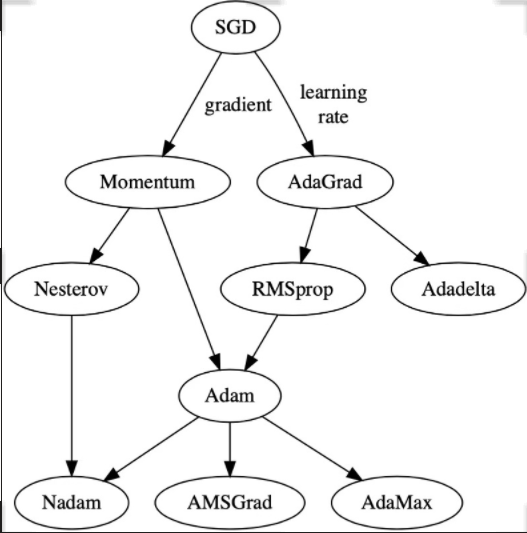
梯度下降

我们前面已经说过很多了，预测函数函数为：

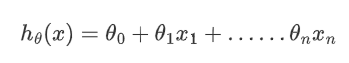
我们使用均方差损失函数：

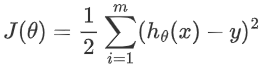
我们的目标是最小化损失函数，我们就对每一个$theta_i$进行求偏导，就可以得到当前轮的梯度，然后损失函数向梯度的反方向更新，不断这样的迭代更新，就可以得到超参数的全局最优解。运用链式求导方法，数学过程可以表示为：

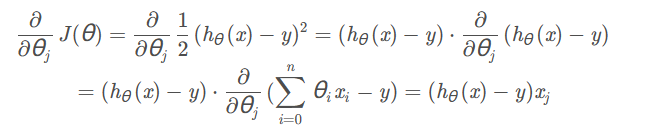
这个梯度表示迭代的速度，我们加上学习率，就得到下面的完整公式:

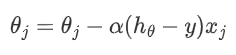
这个地方我们计算好处所有样本的梯度，然后进行累加或者求和。

随机梯度下降

随机梯度下降算法（Stochastic gradient descent，SGD）的公式是这样的：

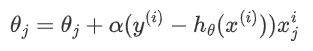
这个算法的流程是在每次更新的时候使用一个样本进行梯度下降，所谓的随机量子，就是说我们可以随机用一个样本代表所有样本，来调整超参数$theta$。

因为这个样本是随机的，所以每次迭代没有办法得到一个准确的梯度，这样一来虽然每一次迭代得到的损失函数不一定是朝着全局最优方向，但是大体的方向还是朝着全局最优解的方向靠近，直到最后，得到的结果通常就会在全局最优解的附近。

优点：

1. 计算开销小：由于每次只使用单个样本的梯度，SGD的计算开销较小，尤其在大规模数据集上更加高效。
2. 内存要求低：无需一次性加载所有训练样本到内存中，使得SGD适用于处理大型数据集。
3. 可以逃离局部最小值：由于更新方向的随机性，SGD有助于跳出局部最小值，更有可能达到全局最优解或接近最优解的位置。

缺点：

1. 不稳定性：由于每次参数更新只使用单个样本的梯度，SGD的参数更新方向较不稳定，可能引起目标函数在优化过程中的波动。
2. 收敛速度较慢：由于参数更新的不稳定性，SGD的收敛速度较慢，可能需要更多的迭代次数才能达到收敛。

小批量梯度下降

小批量梯度下降（Mini-Batch Gradient Descent，MBGD）是梯度下降算法的一种变体，它在每次参数更新时使用一小部分训练样本（称为批量）的梯度来估计参数的更新方向。这样可以在计算效率和参数更新的稳定性之间取得一种平衡。

下面是小批量梯度下降的公式：

假设训练集有m个样本，批量大小为b（通常是一个较小的固定数值），参数向量为θ，损失函数为J(θ)，学习率为α。则小批量梯度下降的更新规则可以表示为：

其中，(X) 表示完整的训练集样本，(y) 表示对应的标签，(b) 是批量大小，(I) 是随机选择的批量样本的索引。

这个公式表示在每次迭代中，随机选择一个批量样本的索引集合 (I)，然后使用这个批量样本计算梯度并更新参数。这样的过程会重复进行，直到达到收敛条件。

在每次迭代中，MBGD会选择一个批量大小的子集样本进行梯度计算和参数更新。这样可以减少计算开销，因为不需要处理所有样本，但仍能保持一定的梯度估计准确性。批量大小的选择是一个权衡，较小的批量大小会增加随机性，可能导致参数更新方向的不稳定性，但能够加速计算速度；较大的批量大小能够减少随机性，但可能增加计算开销。

小批量梯度下降综合了批量梯度下降（使用所有样本）和随机梯度下降（使用单个样本）的优点。它通常是在实践中应用最广泛的梯度下降算法之一，能够在大规模数据集上高效地进行模型训练。

优点：

1. 计算效率高：相比于批量梯度下降，小批量梯度下降在每次迭代中只使用一小部分训练样本，因此计算量较小，可以更快地进行参数更新，尤其在大规模数据集上效果明显。
2. 更稳定的参数更新：与随机梯度下降相比，小批量梯度下降使用了一个批量样本的平均梯度或累加梯度进行参数更新，这样可以减少更新方向的随机性，使参数更新更加稳定。
3. 更好的泛化性能：相比于随机梯度下降，小批量梯度下降在每次迭代中使用了一部分样本，这样可以更好地捕捉数据集的整体特征，有助于提高模型的泛化性能。

缺点：

1. 批量大小的选择问题：小批量梯度下降中批量大小的选择是一个权衡。较小的批量大小可以加速计算速度，但可能导致梯度估计的方差较大；较大的批量大小可以减小梯度估计的方差，但会增加计算开销，并且可能陷入局部最优解。

动量法

我们先来看看动量法来解决一个什么事。动量方法是主要用来解决Hessian矩阵病态条件的问题，就是说梯度高度敏感于参数空间的某些方向。可以用来加速学习，一般将参数设置为0.5，0.9，和0.99分别达到原来速度的2倍，10倍和100倍。并且通过速度v，来积累了之间梯度指数级衰减的平均，并且延续该方向移动。

算法图：

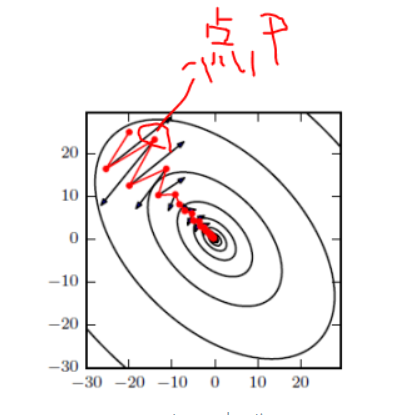
直观解释

如图所示，红色为SGD+Momentum，黑色为SGD，可以看到黑色为典型的Hessian矩阵病态情况，相当于大幅度徘徊着向最低点前进。

由于动量积攒了历史的梯度，如点P前一刻的梯度与当前梯度几乎相反，因此原本在P点原本要大幅度徘徊的梯度，收到前一时刻的影响，导致当前时刻梯度幅度减小。

直观的讲就是，要当前时刻的梯度与历史梯度方向相似，这种趋势在当前时刻会加强，要是不同，则当前时刻梯度方向减弱。

分析

假设每个时刻梯度的g都是类似的，那么我们根据上面的公式$v gets alpha v-epsilon g$可以得到每次的步长为

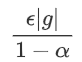
所以$alpha$设置为0.5，0.9和0.99的时候，速度可以是2、10和100倍

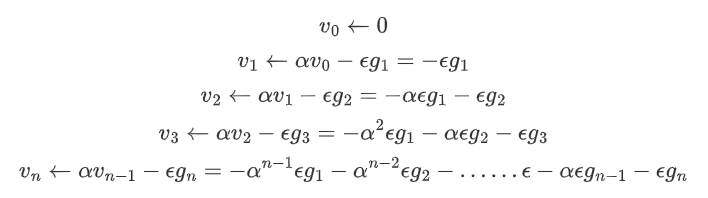
动量法2

当使用动量法时，动量变量$v$的更新可以通过递归的方式得到。假设$t$表示当前的迭代步数，$v_t$表示第$t$步的动量变量，$g_t$表示第$t$步的梯度，$epsilon$表示学习率，$beta$表示动量衰减因子。

动量变量的更新公式为：

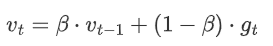
其中，$v_{t-1}$表示上一步的动量变量。

为了得到$v_0$到$v_n$的推导公式，我们可以根据递归关系展开动量变量的更新。首先，我们将$v_0$设为初始动量变量的值，通常为0。然后，根据递归关系，我们可以得到以下推导公式：

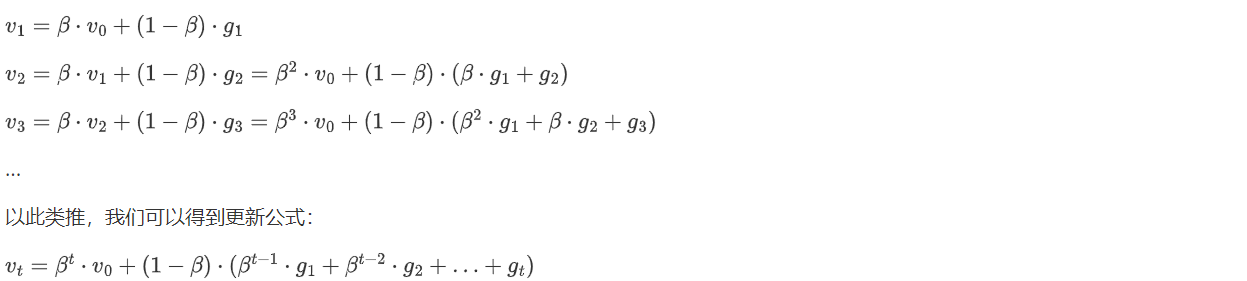
这个公式描述了在$t$步时的动量变量$v_t$的计算方式，其中$v_0$是初始动量变量，$beta$是动量衰减因子，$g_1, g_2, ldots, g_t$是从第一步到第$t$步的梯度。

这个好像是和adam接壤的，那么上面的两个动量法区别是什么呢？

adagrad算法

我们前面的学习率都是规定固定不变的，但是实际上越往后梯度越小，越平缓，很难取得进步，这个时候使用动态调整的adagrad算法可以更快训练模型。

起到的效果是在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度。

算法图：

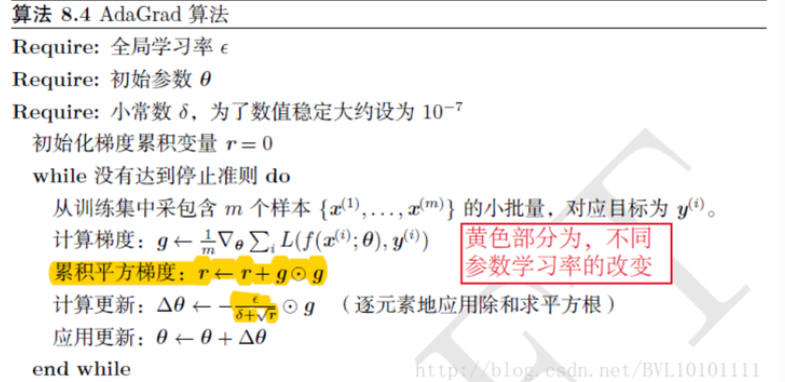
总体来说就是梯度计算方式不变，使用小批量梯度下降算法，更改学习率，学习率从$epsilon$变成了$frac{epsilon}{sqrt{s+r}}$，其中r的作用就是防止代码报错，因为s可能是等于0的，r就是一个很小的值，s是批量内样本梯度平方的累加。

Adagrad 的核心想法就是，如果一个参数的梯度一直都非常大，那么其对应的学习率就变小一点，防止震荡，而一个参数的梯度一直都非常小，那么这个参数的学习率就变大一点，使得其能够更快地更新，这就是Adagrad算法加快深层神经网络的训练速度的核心。

RMSProp算法

RMSprop（Root Mean Square Propagation）是一种优化算法，用于调整神经网络训练中的学习率，就是AdaGrad做了一些变形。

RMSprop的核心思想是使用移动平均来估计梯度的二阶矩（即平方梯度的期望值），并将学习率调整为参数梯度的标准差与移动平均的平方根之比。这样可以使得在参数更新时，对于梯度较大的参数施加较小的学习率，对于梯度较小的参数施加较大的学习率，从而在不同参数之间实现自适应调整。

下面是RMSprop算法的更新公式：

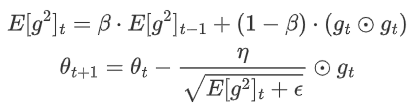
在每次迭代中，RMSprop算法使用移动平均来估计梯度平方的期望值，并将该估计值用于调整学习率。通过除以梯度平方的平方根，可以实现对学习率的自适应调整，以便更好地适应不同参数的梯度变化。

加入了一个历史的参数，暂时不能理解它的意义是什么，这个我需要一个例子。

我想了一下：如果数据集是稀疏的，即每个样本只有少量的非零特征，那么Adagrad可能会表现得更好。因为Adagrad能够对每个参数的梯度进行累积，使得稀疏特征的参数可以得到更大的学习率，从而更好地适应这种情况。

另一方面，如果数据集具有不同特征的梯度变化差异较大，即某些特征的梯度较大，而其他特征的梯度较小，那么RMSprop可能会表现得更好。RMSprop使用了一个移动平均的方式估计梯度平方的期望值，能够自适应地调整学习率。这使得在不同特征的梯度变化差异较大的情况下，RMSprop能够更好地平衡参数更新的速度，使得收敛更快。这个和动量法加入历史记录是一致的。

adam算法